Topic4 - Plotting and Data Visualization

lecture
Author

Harun Pirim

Published

August 14, 2023

Introduction

There might be different goals to visualize networks. Some of them are shown in Figure 1.

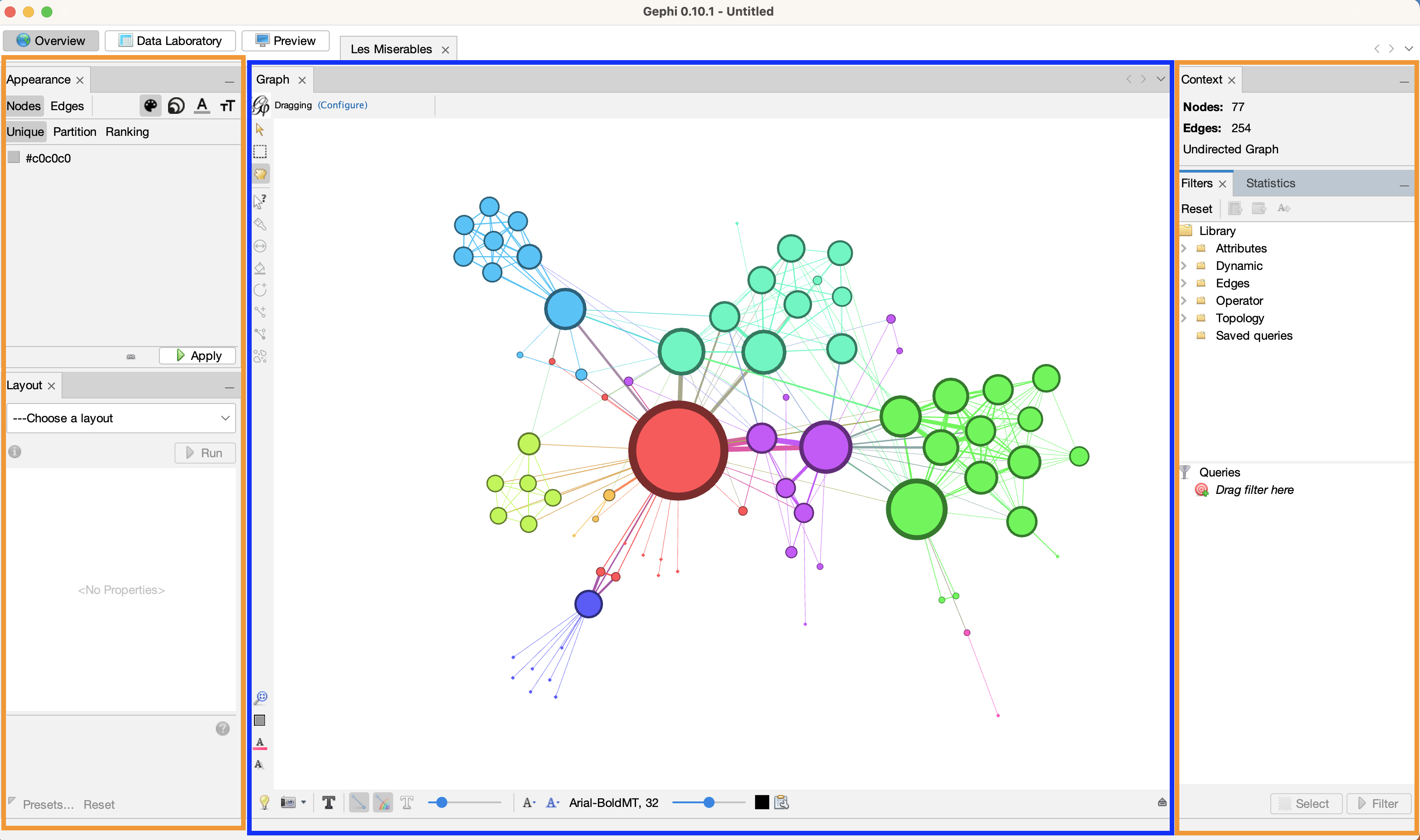
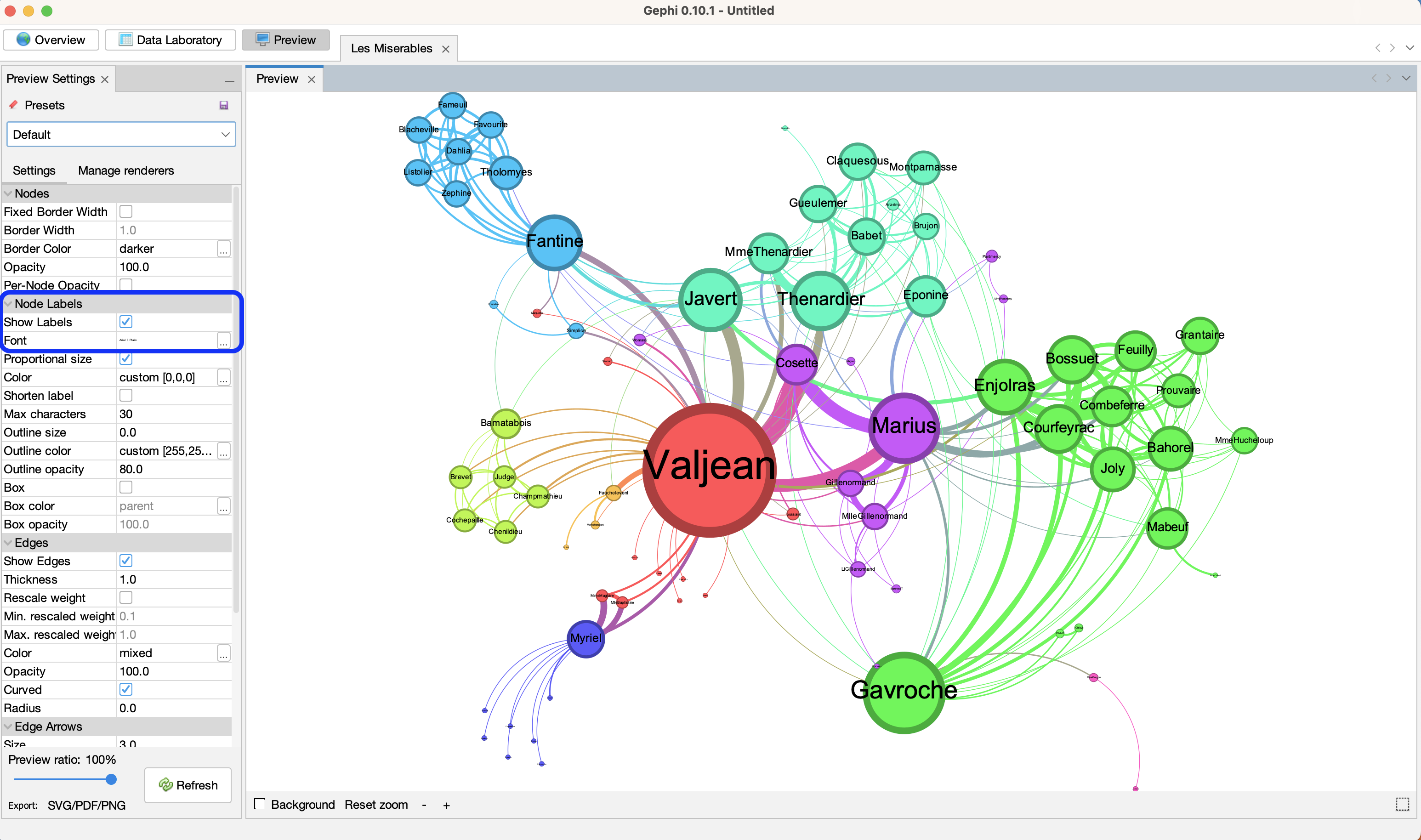
Alt Text
Figure 1: Some of network visualization goals (courtesy of Section 2 Reference 2).
Code 
def draw_graph(G, nodes_position, weight):
    nx.draw(G, nodes_position, with_labels=True, font_size=15,
    node_size=400, edge_color='gray', arrowsize=30)
    if weight:
        edge_labels=nx.get_edge_attributes(G,'weight')
        nx.draw_networkx_edge_labels(G, nodes_position, edge_labels=edge_labels)


import networkx as nx
G = nx.Graph()
V = {'Paris', 'Dublin','Milan', 'Rome'}
E = [('Paris','Dublin', 11), ('Paris','Milan', 8),
('Milan','Rome', 5), ('Milan','Dublin', 19)]
G.add_nodes_from(V)
G.add_weighted_edges_from(E)
node_position = {"Paris": [0,0], "Dublin": [0,1], "Milan":
[1,0], "Rome": [1,1]}
#node_position2 = nx.spring_layout(G)
#node_position3 = nx.circular_layout(G)
#node_position4 = nx.spectral_layout(G)
#node_position5 = nx.shell_layout(G)
#node_position6 = nx.random_layout(G)
#node_position7 = nx.kamada_kawai_layout(G)
#node_position8 = nx.planar_layout(G)
#node_position9 = nx.fruchterman_reingold_layout(G)
#node_position10 = nx.spiral_layout(G)
#node_position11 = nx.multipartite_layout(G)
#node_position12 = nx.bipartite_layout(G, V)
#node_position13 = nx.rescale_layout(G)

draw_graph(G, node_position, True)
/Users/harunpirim/Library/Python/3.9/lib/python/site-packages/networkx/drawing/nx_pylab.py:304: UserWarning: 

The arrowsize keyword argument is not applicable when drawing edges
with LineCollection.

To make this warning go away, either specify `arrows=True` to
force FancyArrowPatches or use the default value for arrowsize.
Note that using FancyArrowPatches may be slow for large graphs.

  draw_networkx_edges(G, pos, arrows=arrows, **edge_kwds)

Alt Text
Figure 2: Various layouts (courtesy of Section 2 Reference 1).

More complex and rich decorations can be obtained using the Gephi software. I used to be a fan of igraph library visualization capabilities. You can check it out in R or Python. However, I will go with Gephi here. You can save nexworkx object in graphML format to be read into Gephi or export Gephi object as graphML to be read into Python. Let’s work on a sample graph in Gephi, les miserables with 77 nodes and 254 edges. Nice visualization!

Alt Text
Figure 3: Gephi panes. Three of them are colored in rectangles.

Under the filters tab, it is possible to filter the graph based on combination of network metrics and statistics. Figure 3 shows added node labels for the graph.

Alt Text
Figure 4: Node labels added and font size is adjusted. See inside the blue rectangle. Notice the edges being curved.

You can color the nodes based on modularity classs (i.e. output of some clustering algorithms) that is computed under the statistics tab. See Figure 5.

Alt Text
Figure 5: Coloring the nodes based on communities.

Once you are done with the visualization, you can export the graph as graphML file. You can read it into Python using networkx library.

Code 
import networkx as nx
# Read GraphML file exported from Gephi
gephi_graph = nx.read_graphml("lesmis.graphml")
# Print the nodes and edges
print("Nodes: ", gephi_graph.nodes())
print("Edges: ", gephi_graph.edges())
# Print names of the nodes
print("Node names: ", [gephi_graph.nodes[node]["label"] for node in gephi_graph.nodes()])
# Print weights of the edges
print("Edge weights: ", [gephi_graph.edges[edge]["weight"] for edge in gephi_graph.edges()])
# add new node attribute (export to graphML file later)
for node in gephi_graph.nodes():
    gephi_graph.nodes[node]["degree"] = gephi_graph.degree(node)
# Print the node attributes
print("Node attributes: ", [gephi_graph.nodes[node] for node in gephi_graph.nodes()])
# Draw the graph (not as nice as Gephi :) output)
nx.draw(gephi_graph, with_labels=True, font_size=15)
# Export the graph as pandas dataframe (nodes and edges)
import pandas as pd
df = nx.to_pandas_edgelist(gephi_graph)
df1 = nx.to_pandas_adjacency(gephi_graph)
print(df)
# Convert the node attributes to pandas dataframe
node_data = []
for node, attributes in gephi_graph.nodes(data=True):
    node_data.append(attributes)
node_df = pd.DataFrame(node_data)
print(node_df)
# dimension of the dataframe
print(node_df.shape)
# Add another node attribute to the dataframe
# Iterate through nodes and their attributes
node_data = []
for node, attributes in gephi_graph.nodes(data=True):
    # Calculate the degree of each node
    degree = gephi_graph.degree(node)
    
    # Add the degree and other attributes to the list
    attributes["degree"] = degree
    node_data.append(attributes)
# Create a pandas DataFrame from the node data
node_df = pd.DataFrame(node_data)
print(node_df.shape)
# Export the dataframe as csv file
node_df.to_csv("lesmisN.csv", index=False)
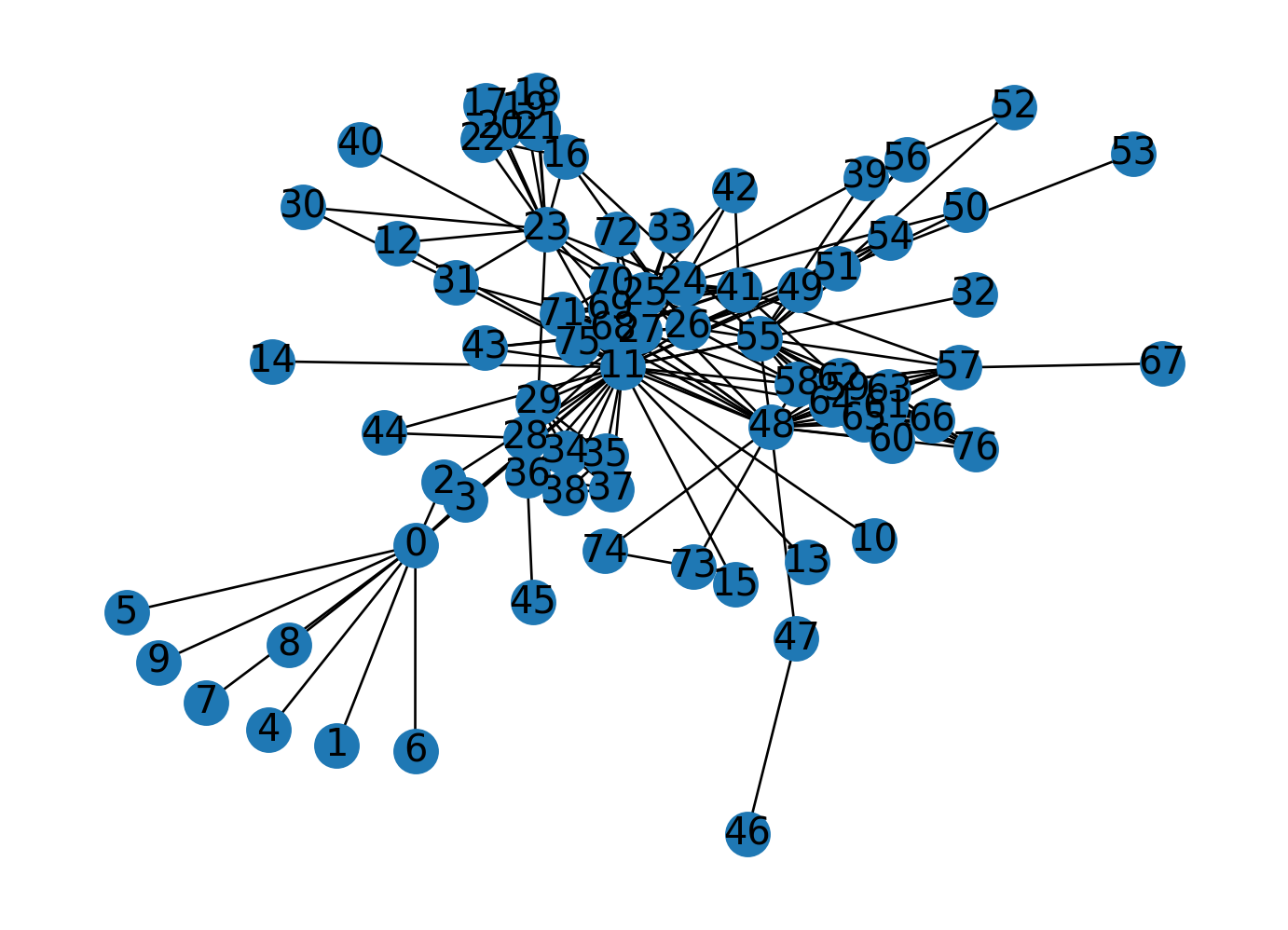
Nodes:  ['11', '48', '55', '27', '25', '23', '58', '62', '64', '63', '65', '24', '26', '41', '57', '59', '61', '0', '66', '68', '69', '70', '16', '60', '71', '29', '17', '18', '19', '20', '21', '22', '49', '51', '75', '76', '34', '35', '36', '37', '38', '28', '31', '54', '2', '3', '39', '42', '43', '72', '12', '30', '33', '44', '47', '50', '52', '56', '73', '74', '1', '4', '5', '6', '7', '8', '9', '10', '13', '14', '15', '32', '40', '45', '46', '53', '67']
Edges:  [('11', '0'), ('11', '2'), ('11', '3'), ('11', '10'), ('11', '12'), ('11', '13'), ('11', '14'), ('11', '15'), ('11', '23'), ('11', '24'), ('11', '25'), ('11', '26'), ('11', '27'), ('11', '28'), ('11', '29'), ('11', '31'), ('11', '32'), ('11', '33'), ('11', '34'), ('11', '35'), ('11', '36'), ('11', '37'), ('11', '38'), ('11', '43'), ('11', '44'), ('11', '48'), ('11', '49'), ('11', '51'), ('11', '55'), ('11', '58'), ('11', '64'), ('11', '68'), ('11', '69'), ('11', '70'), ('11', '71'), ('11', '72'), ('48', '25'), ('48', '27'), ('48', '47'), ('48', '55'), ('48', '57'), ('48', '58'), ('48', '59'), ('48', '60'), ('48', '61'), ('48', '62'), ('48', '63'), ('48', '64'), ('48', '65'), ('48', '66'), ('48', '68'), ('48', '69'), ('48', '71'), ('48', '73'), ('48', '74'), ('48', '75'), ('48', '76'), ('55', '16'), ('55', '25'), ('55', '26'), ('55', '39'), ('55', '41'), ('55', '49'), ('55', '51'), ('55', '54'), ('55', '56'), ('55', '57'), ('55', '58'), ('55', '59'), ('55', '61'), ('55', '62'), ('55', '63'), ('55', '64'), ('55', '65'), ('27', '23'), ('27', '24'), ('27', '25'), ('27', '26'), ('27', '28'), ('27', '29'), ('27', '31'), ('27', '33'), ('27', '43'), ('27', '58'), ('27', '68'), ('27', '69'), ('27', '70'), ('27', '71'), ('27', '72'), ('25', '23'), ('25', '24'), ('25', '26'), ('25', '39'), ('25', '40'), ('25', '41'), ('25', '42'), ('25', '68'), ('25', '69'), ('25', '70'), ('25', '71'), ('25', '75'), ('23', '12'), ('23', '16'), ('23', '17'), ('23', '18'), ('23', '19'), ('23', '20'), ('23', '21'), ('23', '22'), ('23', '24'), ('23', '29'), ('23', '30'), ('23', '31'), ('58', '57'), ('58', '59'), ('58', '60'), ('58', '61'), ('58', '62'), ('58', '63'), ('58', '64'), ('58', '65'), ('58', '66'), ('58', '70'), ('58', '76'), ('62', '41'), ('62', '57'), ('62', '59'), ('62', '60'), ('62', '61'), ('62', '63'), ('62', '64'), ('62', '65'), ('62', '66'), ('62', '76'), ('64', '57'), ('64', '59'), ('64', '60'), ('64', '61'), ('64', '63'), ('64', '65'), ('64', '66'), ('64', '76'), ('63', '57'), ('63', '59'), ('63', '60'), ('63', '61'), ('63', '65'), ('63', '66'), ('63', '76'), ('65', '57'), ('65', '59'), ('65', '60'), ('65', '61'), ('65', '66'), ('65', '76'), ('24', '26'), ('24', '41'), ('24', '42'), ('24', '50'), ('24', '68'), ('24', '69'), ('24', '70'), ('26', '16'), ('26', '43'), ('26', '49'), ('26', '51'), ('26', '54'), ('26', '72'), ('41', '42'), ('41', '57'), ('41', '68'), ('41', '69'), ('41', '70'), ('41', '71'), ('41', '75'), ('57', '59'), ('57', '61'), ('57', '67'), ('59', '60'), ('59', '61'), ('59', '66'), ('61', '60'), ('61', '66'), ('0', '1'), ('0', '2'), ('0', '3'), ('0', '4'), ('0', '5'), ('0', '6'), ('0', '7'), ('0', '8'), ('0', '9'), ('66', '60'), ('66', '76'), ('68', '69'), ('68', '70'), ('68', '71'), ('68', '75'), ('69', '70'), ('69', '71'), ('69', '75'), ('70', '71'), ('70', '75'), ('16', '17'), ('16', '18'), ('16', '19'), ('16', '20'), ('16', '21'), ('16', '22'), ('71', '75'), ('29', '34'), ('29', '35'), ('29', '36'), ('29', '37'), ('29', '38'), ('17', '18'), ('17', '19'), ('17', '20'), ('17', '21'), ('17', '22'), ('18', '19'), ('18', '20'), ('18', '21'), ('18', '22'), ('19', '20'), ('19', '21'), ('19', '22'), ('20', '21'), ('20', '22'), ('21', '22'), ('49', '50'), ('49', '51'), ('49', '54'), ('49', '56'), ('51', '52'), ('51', '53'), ('51', '54'), ('34', '35'), ('34', '36'), ('34', '37'), ('34', '38'), ('35', '36'), ('35', '37'), ('35', '38'), ('36', '37'), ('36', '38'), ('37', '38'), ('28', '44'), ('28', '45'), ('31', '30'), ('2', '3'), ('39', '52'), ('47', '46'), ('73', '74')]
Node names:  ['Valjean', 'Gavroche', 'Marius', 'Javert', 'Thenardier', 'Fantine', 'Enjolras', 'Courfeyrac', 'Bossuet', 'Bahorel', 'Joly', 'MmeThenardier', 'Cosette', 'Eponine', 'Mabeuf', 'Combeferre', 'Feuilly', 'Myriel', 'Grantaire', 'Gueulemer', 'Babet', 'Claquesous', 'Tholomyes', 'Prouvaire', 'Montparnasse', 'Bamatabois', 'Listolier', 'Fameuil', 'Blacheville', 'Favourite', 'Dahlia', 'Zephine', 'Gillenormand', 'MlleGillenormand', 'Brujon', 'MmeHucheloup', 'Judge', 'Champmathieu', 'Brevet', 'Chenildieu', 'Cochepaille', 'Fauchelevent', 'Simplice', 'LtGillenormand', 'MlleBaptistine', 'MmeMagloire', 'Pontmercy', 'Anzelma', 'Woman2', 'Toussaint', 'Marguerite', 'Perpetue', 'Woman1', 'MotherInnocent', 'MmeBurgon', 'Magnon', 'MmePontmercy', 'BaronessT', 'Child1', 'Child2', 'Napoleon', 'CountessDeLo', 'Geborand', 'Champtercier', 'Cravatte', 'Count', 'OldMan', 'Labarre', 'MmeDeR', 'Isabeau', 'Gervais', 'Scaufflaire', 'Boulatruelle', 'Gribier', 'Jondrette', 'MlleVaubois', 'MotherPlutarch']
Edge weights:  [5.0, 3.0, 3.0, 1.0, 1.0, 1.0, 1.0, 1.0, 9.0, 7.0, 12.0, 31.0, 17.0, 8.0, 2.0, 3.0, 1.0, 2.0, 3.0, 3.0, 2.0, 2.0, 2.0, 3.0, 1.0, 1.0, 2.0, 2.0, 19.0, 4.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 2.0, 4.0, 1.0, 7.0, 6.0, 1.0, 2.0, 7.0, 5.0, 5.0, 3.0, 1.0, 1.0, 1.0, 1.0, 2.0, 2.0, 1.0, 1.0, 1.0, 2.0, 21.0, 1.0, 5.0, 12.0, 6.0, 1.0, 1.0, 1.0, 7.0, 5.0, 1.0, 9.0, 1.0, 5.0, 2.0, 5.0, 1.0, 5.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 6.0, 1.0, 2.0, 1.0, 1.0, 1.0, 1.0, 13.0, 1.0, 1.0, 1.0, 3.0, 2.0, 5.0, 6.0, 4.0, 1.0, 3.0, 2.0, 3.0, 3.0, 3.0, 3.0, 4.0, 4.0, 4.0, 2.0, 1.0, 1.0, 2.0, 1.0, 15.0, 4.0, 6.0, 17.0, 4.0, 10.0, 5.0, 3.0, 1.0, 1.0, 1.0, 2.0, 13.0, 3.0, 6.0, 6.0, 12.0, 5.0, 2.0, 1.0, 1.0, 9.0, 2.0, 6.0, 4.0, 7.0, 3.0, 1.0, 2.0, 5.0, 2.0, 3.0, 5.0, 1.0, 1.0, 1.0, 5.0, 2.0, 5.0, 2.0, 1.0, 4.0, 2.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 3.0, 2.0, 1.0, 2.0, 2.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 2.0, 1.0, 3.0, 2.0, 5.0, 1.0, 2.0, 1.0, 1.0, 8.0, 10.0, 1.0, 1.0, 1.0, 1.0, 2.0, 1.0, 1.0, 1.0, 6.0, 4.0, 2.0, 3.0, 4.0, 2.0, 3.0, 2.0, 1.0, 4.0, 4.0, 4.0, 3.0, 3.0, 3.0, 1.0, 2.0, 2.0, 1.0, 1.0, 1.0, 4.0, 4.0, 3.0, 3.0, 3.0, 4.0, 3.0, 3.0, 3.0, 4.0, 3.0, 3.0, 5.0, 4.0, 4.0, 1.0, 9.0, 1.0, 1.0, 1.0, 1.0, 2.0, 3.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 3.0, 2.0, 2.0, 6.0, 1.0, 1.0, 3.0]
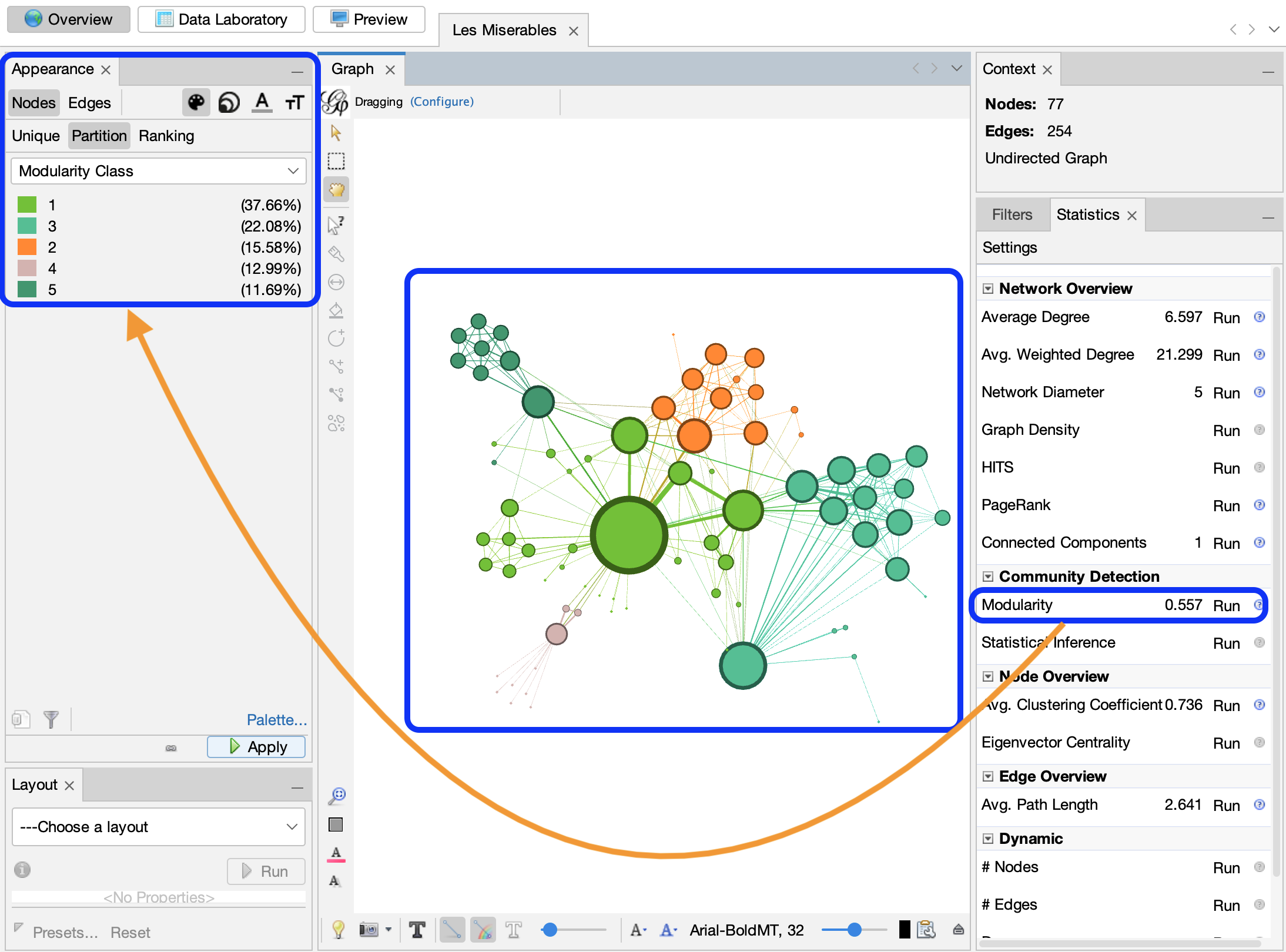
Node attributes:  [{'label': 'Valjean', 'Modularity Class': 1, 'Clustering Coefficient': 0.12063492063492064, 'Number of triangles': 76, 'Eccentricity': 3.0, 'Closeness Centrality': 0.6440677966101694, 'Harmonic Closeness Centrality': 0.7324561403508772, 'Betweenness Centrality': 0.5699890527836187, 'Degree': 36, 'Weighted Degree': 158.0, 'PageRank': 0.09965386050164989, 'Component ID': 0, 'size': 31.0, 'r': 115, 'g': 192, 'b': 0, 'x': -125.47393, 'y': -77.948814, 'degree': 36}, {'label': 'Gavroche', 'Modularity Class': 3, 'Clustering Coefficient': 0.354978354978355, 'Number of triangles': 82, 'Eccentricity': 3.0, 'Closeness Centrality': 0.5135135135135135, 'Harmonic Closeness Centrality': 0.6052631578947372, 'Betweenness Centrality': 0.16511250242584768, 'Degree': 22, 'Weighted Degree': 56.0, 'PageRank': 0.02825608878181585, 'Component ID': 0, 'size': 17.356688, 'r': 0, 'g': 189, 'b': 148, 'x': 468.20163, 'y': 19.530542, 'degree': 22}, {'label': 'Marius', 'Modularity Class': 1, 'Clustering Coefficient': 0.3333333333333333, 'Number of triangles': 57, 'Eccentricity': 3.0, 'Closeness Centrality': 0.5314685314685315, 'Harmonic Closeness Centrality': 0.6030701754385968, 'Betweenness Centrality': 0.13203248862194603, 'Degree': 19, 'Weighted Degree': 104.0, 'PageRank': 0.051657080037054555, 'Component ID': 0, 'size': 23.777071, 'r': 115, 'g': 192, 'b': 0, 'x': 354.36575, 'y': 180.87674, 'degree': 19}, {'label': 'Javert', 'Modularity Class': 1, 'Clustering Coefficient': 0.3235294117647059, 'Number of triangles': 44, 'Eccentricity': 3.0, 'Closeness Centrality': 0.5170068027210885, 'Harmonic Closeness Centrality': 0.585526315789474, 'Betweenness Centrality': 0.05433155966478438, 'Degree': 17, 'Weighted Degree': 47.0, 'PageRank': 0.02683696145593788, 'Component ID': 0, 'size': 16.152866, 'r': 115, 'g': 192, 'b': 0, 'x': -234.89421, 'y': 102.36227, 'degree': 17}, {'label': 'Thenardier', 'Modularity Class': 2, 'Clustering Coefficient': 0.4083333333333333, 'Number of triangles': 49, 'Eccentricity': 3.0, 'Closeness Centrality': 0.5170068027210885, 'Harmonic Closeness Centrality': 0.5811403508771933, 'Betweenness Centrality': 0.07490122123424223, 'Degree': 16, 'Weighted Degree': 61.0, 'PageRank': 0.03570364480815213, 'Component ID': 0, 'size': 18.025478, 'r': 255, 'g': 136, 'b': 5, 'x': 131.99199, 'y': 460.77588, 'degree': 16}, {'label': 'Fantine', 'Modularity Class': 5, 'Clustering Coefficient': 0.3142857142857143, 'Number of triangles': 33, 'Eccentricity': 4.0, 'Closeness Centrality': 0.46060606060606063, 'Harmonic Closeness Centrality': 0.5394736842105267, 'Betweenness Centrality': 0.12964454098819433, 'Degree': 15, 'Weighted Degree': 47.0, 'PageRank': 0.027169003618714563, 'Component ID': 0, 'size': 16.152866, 'r': 35, 'g': 150, 'b': 111, 'x': -271.28757, 'y': 424.28168, 'degree': 15}, {'label': 'Enjolras', 'Modularity Class': 3, 'Clustering Coefficient': 0.6095238095238096, 'Number of triangles': 64, 'Eccentricity': 3.0, 'Closeness Centrality': 0.4810126582278481, 'Harmonic Closeness Centrality': 0.5526315789473687, 'Betweenness Centrality': 0.04255335682217709, 'Degree': 15, 'Weighted Degree': 91.0, 'PageRank': 0.03654226925514488, 'Component ID': 0, 'size': 22.038216, 'r': 0, 'g': 189, 'b': 148, 'x': 289.11673, 'y': -9.404579, 'degree': 15}, {'label': 'Courfeyrac', 'Modularity Class': 3, 'Clustering Coefficient': 0.7564102564102564, 'Number of triangles': 59, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4, 'Harmonic Closeness Centrality': 0.4835526315789473, 'Betweenness Centrality': 0.005267029881988329, 'Degree': 13, 'Weighted Degree': 84.0, 'PageRank': 0.032920423413624826, 'Component ID': 0, 'size': 21.101912, 'r': 0, 'g': 189, 'b': 148, 'x': 524.805, 'y': 262.02774, 'degree': 13}, {'label': 'Bossuet', 'Modularity Class': 3, 'Clustering Coefficient': 0.7692307692307693, 'Number of triangles': 60, 'Eccentricity': 3.0, 'Closeness Centrality': 0.475, 'Harmonic Closeness Centrality': 0.5394736842105265, 'Betweenness Centrality': 0.030753650179957823, 'Degree': 13, 'Weighted Degree': 66.0, 'PageRank': 0.02613147881051923, 'Component ID': 0, 'size': 18.694267, 'r': 0, 'g': 189, 'b': 148, 'x': 637.1706, 'y': 133.8224, 'degree': 13}, {'label': 'Bahorel', 'Modularity Class': 3, 'Clustering Coefficient': 0.8636363636363636, 'Number of triangles': 57, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.4725877192982455, 'Betweenness Centrality': 0.0021854883087570063, 'Degree': 12, 'Weighted Degree': 39.0, 'PageRank': 0.01641176743972916, 'Component ID': 0, 'size': 15.082803, 'r': 0, 'g': 189, 'b': 148, 'x': 442.76276, 'y': -163.00533, 'degree': 12}, {'label': 'Joly', 'Modularity Class': 3, 'Clustering Coefficient': 0.8636363636363636, 'Number of triangles': 57, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.4725877192982455, 'Betweenness Centrality': 0.0021854883087570063, 'Degree': 12, 'Weighted Degree': 43.0, 'PageRank': 0.017626550302914216, 'Component ID': 0, 'size': 15.617834, 'r': 0, 'g': 189, 'b': 148, 'x': 661.54456, 'y': -42.901436, 'degree': 12}, {'label': 'MmeThenardier', 'Modularity Class': 2, 'Clustering Coefficient': 0.4909090909090909, 'Number of triangles': 27, 'Eccentricity': 4.0, 'Closeness Centrality': 0.46060606060606063, 'Harmonic Closeness Centrality': 0.5208333333333336, 'Betweenness Centrality': 0.029002418730461742, 'Degree': 11, 'Weighted Degree': 34.0, 'PageRank': 0.020052671309919806, 'Component ID': 0, 'size': 14.414013, 'r': 255, 'g': 136, 'b': 5, 'x': -149.65874, 'y': 270.2928, 'degree': 11}, {'label': 'Cosette', 'Modularity Class': 1, 'Clustering Coefficient': 0.38181818181818183, 'Number of triangles': 21, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4779874213836478, 'Harmonic Closeness Centrality': 0.5339912280701757, 'Betweenness Centrality': 0.02379625345414818, 'Degree': 11, 'Weighted Degree': 68.0, 'PageRank': 0.03693341783802389, 'Component ID': 0, 'size': 18.961784, 'r': 115, 'g': 192, 'b': 0, 'x': -37.07721, 'y': 99.6509, 'degree': 11}, {'label': 'Eponine', 'Modularity Class': 2, 'Clustering Coefficient': 0.45454545454545453, 'Number of triangles': 25, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3958333333333333, 'Harmonic Closeness Centrality': 0.4703947368421051, 'Betweenness Centrality': 0.011487550654163006, 'Degree': 11, 'Weighted Degree': 19.0, 'PageRank': 0.011544867855978474, 'Component ID': 0, 'size': 12.407643, 'r': 255, 'g': 136, 'b': 5, 'x': 333.57504, 'y': 538.7558, 'degree': 11}, {'label': 'Mabeuf', 'Modularity Class': 3, 'Clustering Coefficient': 0.6909090909090909, 'Number of triangles': 38, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3958333333333333, 'Harmonic Closeness Centrality': 0.47039473684210514, 'Betweenness Centrality': 0.02766123642439432, 'Degree': 11, 'Weighted Degree': 16.0, 'PageRank': 0.009698830968589355, 'Component ID': 0, 'size': 12.00637, 'r': 0, 'g': 189, 'b': 148, 'x': 501.20184, 'y': 433.59323, 'degree': 11}, {'label': 'Combeferre', 'Modularity Class': 3, 'Clustering Coefficient': 0.9272727272727272, 'Number of triangles': 51, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3917525773195876, 'Harmonic Closeness Centrality': 0.46600877192982443, 'Betweenness Centrality': 0.0012501455659350397, 'Degree': 11, 'Weighted Degree': 68.0, 'PageRank': 0.026565292013165664, 'Component ID': 0, 'size': 18.961784, 'r': 0, 'g': 189, 'b': 148, 'x': 816.9591, 'y': 207.98074, 'degree': 11}, {'label': 'Feuilly', 'Modularity Class': 3, 'Clustering Coefficient': 0.9272727272727272, 'Number of triangles': 51, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3917525773195876, 'Harmonic Closeness Centrality': 0.46600877192982443, 'Betweenness Centrality': 0.0012501455659350397, 'Degree': 11, 'Weighted Degree': 38.0, 'PageRank': 0.015454968887759603, 'Component ID': 0, 'size': 14.949045, 'r': 0, 'g': 189, 'b': 148, 'x': 720.7003, 'y': 352.84946, 'degree': 11}, {'label': 'Myriel', 'Modularity Class': 4, 'Clustering Coefficient': 0.06666666666666667, 'Number of triangles': 3, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4293785310734463, 'Harmonic Closeness Centrality': 0.4912280701754386, 'Betweenness Centrality': 0.17684210526315788, 'Degree': 10, 'Weighted Degree': 31.0, 'PageRank': 0.03934482687947826, 'Component ID': 0, 'size': 14.012739, 'r': 211, 'g': 179, 'b': 176, 'x': -337.2892, 'y': -582.49884, 'degree': 10}, {'label': 'Grantaire', 'Modularity Class': 3, 'Clustering Coefficient': 0.9333333333333333, 'Number of triangles': 42, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3584905660377358, 'Harmonic Closeness Centrality': 0.4320175438596488, 'Betweenness Centrality': 0.00015037593984962405, 'Degree': 10, 'Weighted Degree': 16.0, 'PageRank': 0.007736170730043202, 'Component ID': 0, 'size': 12.00637, 'r': 0, 'g': 189, 'b': 148, 'x': 633.325, 'y': -216.78468, 'degree': 10}, {'label': 'Gueulemer', 'Modularity Class': 2, 'Clustering Coefficient': 0.8, 'Number of triangles': 36, 'Eccentricity': 3.0, 'Closeness Centrality': 0.4634146341463415, 'Harmonic Closeness Centrality': 0.517543859649123, 'Betweenness Centrality': 0.00496038397838952, 'Degree': 10, 'Weighted Degree': 25.0, 'PageRank': 0.01469334248583409, 'Component ID': 0, 'size': 13.210192, 'r': 255, 'g': 136, 'b': 5, 'x': 85.83904, 'y': -31.910248, 'degree': 10}, {'label': 'Babet', 'Modularity Class': 2, 'Clustering Coefficient': 0.8, 'Number of triangles': 36, 'Eccentricity': 3.0, 'Closeness Centrality': 0.4634146341463415, 'Harmonic Closeness Centrality': 0.517543859649123, 'Betweenness Centrality': 0.00496038397838952, 'Degree': 10, 'Weighted Degree': 27.0, 'PageRank': 0.015706919998435293, 'Component ID': 0, 'size': 13.477707, 'r': 255, 'g': 136, 'b': 5, 'x': 53.911106, 'y': 291.22214, 'degree': 10}, {'label': 'Claquesous', 'Modularity Class': 2, 'Clustering Coefficient': 0.7111111111111111, 'Number of triangles': 32, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4523809523809524, 'Harmonic Closeness Centrality': 0.5098684210526317, 'Betweenness Centrality': 0.004861804195599211, 'Degree': 10, 'Weighted Degree': 20.0, 'PageRank': 0.011977208955623297, 'Component ID': 0, 'size': 12.541401, 'r': 255, 'g': 136, 'b': 5, 'x': -66.46809, 'y': 446.9708, 'degree': 10}, {'label': 'Tholomyes', 'Modularity Class': 5, 'Clustering Coefficient': 0.6111111111111112, 'Number of triangles': 22, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3917525773195876, 'Harmonic Closeness Centrality': 0.45723684210526305, 'Betweenness Centrality': 0.040629348177335795, 'Degree': 9, 'Weighted Degree': 26.0, 'PageRank': 0.014063075040720454, 'Component ID': 0, 'size': 13.343949, 'r': 35, 'g': 150, 'b': 111, 'x': -10.541667, 'y': 636.56775, 'degree': 9}, {'label': 'Prouvaire', 'Modularity Class': 3, 'Clustering Coefficient': 1.0, 'Number of triangles': 36, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3568075117370892, 'Harmonic Closeness Centrality': 0.4254385964912277, 'Betweenness Centrality': 0.0, 'Degree': 9, 'Weighted Degree': 19.0, 'PageRank': 0.008588735565046515, 'Component ID': 0, 'size': 12.407643, 'r': 0, 'g': 189, 'b': 148, 'x': 842.0357, 'y': 18.039314, 'degree': 9}, {'label': 'Montparnasse', 'Modularity Class': 2, 'Clustering Coefficient': 0.8333333333333334, 'Number of triangles': 30, 'Eccentricity': 3.0, 'Closeness Centrality': 0.4578313253012048, 'Harmonic Closeness Centrality': 0.5087719298245615, 'Betweenness Centrality': 0.003873829873829876, 'Degree': 9, 'Weighted Degree': 12.0, 'PageRank': 0.007971088110553802, 'Component ID': 0, 'size': 11.471337, 'r': 255, 'g': 136, 'b': 5, 'x': 166.81331, 'y': 159.88414, 'degree': 9}, {'label': 'Bamatabois', 'Modularity Class': 1, 'Clustering Coefficient': 0.6428571428571429, 'Number of triangles': 18, 'Eccentricity': 4.0, 'Closeness Centrality': 0.42696629213483145, 'Harmonic Closeness Centrality': 0.4802631578947367, 'Betweenness Centrality': 0.00804093567251462, 'Degree': 8, 'Weighted Degree': 11.0, 'PageRank': 0.00892584056885115, 'Component ID': 0, 'size': 11.33758, 'r': 115, 'g': 192, 'b': 0, 'x': -449.2899, 'y': 89.31822, 'degree': 8}, {'label': 'Listolier', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 5.0, 'Closeness Centrality': 0.34080717488789236, 'Harmonic Closeness Centrality': 0.396271929824561, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 24.0, 'PageRank': 0.013154637140564564, 'Component ID': 0, 'size': 13.076433, 'r': 35, 'g': 150, 'b': 111, 'x': -376.23947, 'y': 760.54596, 'degree': 7}, {'label': 'Fameuil', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 5.0, 'Closeness Centrality': 0.34080717488789236, 'Harmonic Closeness Centrality': 0.396271929824561, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 24.0, 'PageRank': 0.013154637140564564, 'Component ID': 0, 'size': 13.076433, 'r': 35, 'g': 150, 'b': 111, 'x': -14.513618, 'y': 830.6918, 'degree': 7}, {'label': 'Blacheville', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 5.0, 'Closeness Centrality': 0.34080717488789236, 'Harmonic Closeness Centrality': 0.396271929824561, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 25.0, 'PageRank': 0.013626746009166493, 'Component ID': 0, 'size': 13.210192, 'r': 35, 'g': 150, 'b': 111, 'x': -194.7703, 'y': 818.3663, 'degree': 7}, {'label': 'Favourite', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 5.0, 'Closeness Centrality': 0.34080717488789236, 'Harmonic Closeness Centrality': 0.396271929824561, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 26.0, 'PageRank': 0.014127534789476981, 'Component ID': 0, 'size': 13.343949, 'r': 35, 'g': 150, 'b': 111, 'x': -194.94757, 'y': 625.1266, 'degree': 7}, {'label': 'Dahlia', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 5.0, 'Closeness Centrality': 0.34080717488789236, 'Harmonic Closeness Centrality': 0.396271929824561, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 25.0, 'PageRank': 0.013652671093399437, 'Component ID': 0, 'size': 13.210192, 'r': 35, 'g': 150, 'b': 111, 'x': -381.1209, 'y': 570.07184, 'degree': 7}, {'label': 'Zephine', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 5.0, 'Closeness Centrality': 0.34080717488789236, 'Harmonic Closeness Centrality': 0.396271929824561, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 24.0, 'PageRank': 0.013180432974899507, 'Component ID': 0, 'size': 13.076433, 'r': 35, 'g': 150, 'b': 111, 'x': -549.88995, 'y': 643.0912, 'degree': 7}, {'label': 'Gillenormand', 'Modularity Class': 1, 'Clustering Coefficient': 0.47619047619047616, 'Number of triangles': 10, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4418604651162791, 'Harmonic Closeness Centrality': 0.4879385964912281, 'Betweenness Centrality': 0.02021062158319776, 'Degree': 7, 'Weighted Degree': 29.0, 'PageRank': 0.01830834717214438, 'Component ID': 0, 'size': 13.745223, 'r': 115, 'g': 192, 'b': 0, 'x': 143.41684, 'y': -392.82336, 'degree': 7}, {'label': 'MlleGillenormand', 'Modularity Class': 1, 'Clustering Coefficient': 0.42857142857142855, 'Number of triangles': 9, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4418604651162791, 'Harmonic Closeness Centrality': 0.487938596491228, 'Betweenness Centrality': 0.04759892787524366, 'Degree': 7, 'Weighted Degree': 23.0, 'PageRank': 0.01668366272529147, 'Component ID': 0, 'size': 12.942675, 'r': 115, 'g': 192, 'b': 0, 'x': 215.71204, 'y': -185.20508, 'degree': 7}, {'label': 'Brujon', 'Modularity Class': 2, 'Clustering Coefficient': 0.9047619047619048, 'Number of triangles': 19, 'Eccentricity': 4.0, 'Closeness Centrality': 0.38, 'Harmonic Closeness Centrality': 0.4353070175438592, 'Betweenness Centrality': 0.0004385964912280702, 'Degree': 7, 'Weighted Degree': 13.0, 'PageRank': 0.008442262963518268, 'Component ID': 0, 'size': 11.605096, 'r': 255, 'g': 136, 'b': 5, 'x': 291.7335, 'y': 355.01096, 'degree': 7}, {'label': 'MmeHucheloup', 'Modularity Class': 3, 'Clustering Coefficient': 1.0, 'Number of triangles': 21, 'Eccentricity': 4.0, 'Closeness Centrality': 0.35348837209302325, 'Harmonic Closeness Centrality': 0.4122807017543856, 'Betweenness Centrality': 0.0, 'Degree': 7, 'Weighted Degree': 7.0, 'PageRank': 0.004503289752419272, 'Component ID': 0, 'size': 10.802547, 'r': 0, 'g': 189, 'b': 148, 'x': 517.6278, 'y': -362.45767, 'degree': 7}, {'label': 'Judge', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 15, 'Eccentricity': 4.0, 'Closeness Centrality': 0.40425531914893614, 'Harmonic Closeness Centrality': 0.44956140350877183, 'Betweenness Centrality': 0.0, 'Degree': 6, 'Weighted Degree': 14.0, 'PageRank': 0.011347466475910712, 'Component ID': 0, 'size': 11.738853, 'r': 115, 'g': 192, 'b': 0, 'x': -590.1966, 'y': 252.0168, 'degree': 6}, {'label': 'Champmathieu', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 15, 'Eccentricity': 4.0, 'Closeness Centrality': 0.40425531914893614, 'Harmonic Closeness Centrality': 0.44956140350877183, 'Betweenness Centrality': 0.0, 'Degree': 6, 'Weighted Degree': 14.0, 'PageRank': 0.011347466475910712, 'Component ID': 0, 'size': 11.738853, 'r': 115, 'g': 192, 'b': 0, 'x': -645.0462, 'y': 75.57544, 'degree': 6}, {'label': 'Brevet', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 15, 'Eccentricity': 4.0, 'Closeness Centrality': 0.40425531914893614, 'Harmonic Closeness Centrality': 0.44956140350877183, 'Betweenness Centrality': 0.0, 'Degree': 6, 'Weighted Degree': 11.0, 'PageRank': 0.009362839598644278, 'Component ID': 0, 'size': 11.33758, 'r': 115, 'g': 192, 'b': 0, 'x': -766.7008, 'y': 324.3104, 'degree': 6}, {'label': 'Chenildieu', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 15, 'Eccentricity': 4.0, 'Closeness Centrality': 0.40425531914893614, 'Harmonic Closeness Centrality': 0.44956140350877183, 'Betweenness Centrality': 0.0, 'Degree': 6, 'Weighted Degree': 11.0, 'PageRank': 0.009362839598644278, 'Component ID': 0, 'size': 11.33758, 'r': 115, 'g': 192, 'b': 0, 'x': -677.83527, 'y': -108.4514, 'degree': 6}, {'label': 'Cochepaille', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 15, 'Eccentricity': 4.0, 'Closeness Centrality': 0.40425531914893614, 'Harmonic Closeness Centrality': 0.44956140350877183, 'Betweenness Centrality': 0.0, 'Degree': 6, 'Weighted Degree': 11.0, 'PageRank': 0.009362839598644278, 'Component ID': 0, 'size': 11.33758, 'r': 115, 'g': 192, 'b': 0, 'x': -821.2932, 'y': 149.76526, 'degree': 6}, {'label': 'Fauchelevent', 'Modularity Class': 1, 'Clustering Coefficient': 0.3333333333333333, 'Number of triangles': 2, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4021164021164021, 'Harmonic Closeness Centrality': 0.43859649122807004, 'Betweenness Centrality': 0.026491228070175437, 'Degree': 4, 'Weighted Degree': 14.0, 'PageRank': 0.0127651648272099, 'Component ID': 0, 'size': 11.738853, 'r': 115, 'g': 192, 'b': 0, 'x': -494.7896, 'y': -107.26308, 'degree': 4}, {'label': 'Simplice', 'Modularity Class': 1, 'Clustering Coefficient': 0.6666666666666666, 'Number of triangles': 4, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4175824175824176, 'Harmonic Closeness Centrality': 0.45394736842105243, 'Betweenness Centrality': 0.008640295033483887, 'Degree': 4, 'Weighted Degree': 8.0, 'PageRank': 0.0072849440410346095, 'Component ID': 0, 'size': 10.936306, 'r': 115, 'g': 192, 'b': 0, 'x': -375.3533, 'y': 261.5612, 'degree': 4}, {'label': 'LtGillenormand', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 6, 'Eccentricity': 4.0, 'Closeness Centrality': 0.36538461538461536, 'Harmonic Closeness Centrality': 0.4057017543859646, 'Betweenness Centrality': 0.0, 'Degree': 4, 'Weighted Degree': 5.0, 'PageRank': 0.004601842348910095, 'Component ID': 0, 'size': 10.535032, 'r': 115, 'g': 192, 'b': 0, 'x': 322.52313, 'y': -337.14368, 'degree': 4}, {'label': 'MlleBaptistine', 'Modularity Class': 4, 'Clustering Coefficient': 1.0, 'Number of triangles': 3, 'Eccentricity': 4.0, 'Closeness Centrality': 0.41304347826086957, 'Harmonic Closeness Centrality': 0.4451754385964913, 'Betweenness Centrality': 0.0, 'Degree': 3, 'Weighted Degree': 17.0, 'PageRank': 0.01745923045918461, 'Component ID': 0, 'size': 12.140127, 'r': 211, 'g': 179, 'b': 176, 'x': -462.47998, 'y': -441.44427, 'degree': 3}, {'label': 'MmeMagloire', 'Modularity Class': 4, 'Clustering Coefficient': 1.0, 'Number of triangles': 3, 'Eccentricity': 4.0, 'Closeness Centrality': 0.41304347826086957, 'Harmonic Closeness Centrality': 0.4451754385964913, 'Betweenness Centrality': 0.0, 'Degree': 3, 'Weighted Degree': 19.0, 'PageRank': 0.019595413691521003, 'Component ID': 0, 'size': 12.407643, 'r': 211, 'g': 179, 'b': 176, 'x': -143.30481, 'y': -623.2299, 'degree': 3}, {'label': 'Pontmercy', 'Modularity Class': 2, 'Clustering Coefficient': 0.3333333333333333, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.37254901960784315, 'Harmonic Closeness Centrality': 0.4089912280701751, 'Betweenness Centrality': 0.00692543859649123, 'Degree': 3, 'Weighted Degree': 3.0, 'PageRank': 0.004499691448335435, 'Component ID': 0, 'size': 10.267516, 'r': 255, 'g': 136, 'b': 5, 'x': 369.61102, 'y': 752.66266, 'degree': 3}, {'label': 'Anzelma', 'Modularity Class': 2, 'Clustering Coefficient': 1.0, 'Number of triangles': 3, 'Eccentricity': 4.0, 'Closeness Centrality': 0.35185185185185186, 'Harmonic Closeness Centrality': 0.3837719298245611, 'Betweenness Centrality': 0.0, 'Degree': 3, 'Weighted Degree': 5.0, 'PageRank': 0.004477640269040657, 'Component ID': 0, 'size': 10.535032, 'r': 255, 'g': 136, 'b': 5, 'x': 180.48619, 'y': 654.3621, 'degree': 3}, {'label': 'Woman2', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 3, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4021164021164021, 'Harmonic Closeness Centrality': 0.43421052631578927, 'Betweenness Centrality': 0.0, 'Degree': 3, 'Weighted Degree': 5.0, 'PageRank': 0.004504115046356716, 'Component ID': 0, 'size': 10.535032, 'r': 115, 'g': 192, 'b': 0, 'x': -312.96292, 'y': -79.41935, 'degree': 3}, {'label': 'Toussaint', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 3, 'Eccentricity': 4.0, 'Closeness Centrality': 0.4021164021164021, 'Harmonic Closeness Centrality': 0.43421052631578927, 'Betweenness Centrality': 0.0, 'Degree': 3, 'Weighted Degree': 4.0, 'PageRank': 0.003893272260869402, 'Component ID': 0, 'size': 10.401274, 'r': 115, 'g': 192, 'b': 0, 'x': -165.86977, 'y': -260.81754, 'degree': 3}, {'label': 'Marguerite', 'Modularity Class': 5, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.41304347826086957, 'Harmonic Closeness Centrality': 0.44078947368421034, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 3.0, 'PageRank': 0.003467074199557231, 'Component ID': 0, 'size': 10.267516, 'r': 35, 'g': 150, 'b': 111, 'x': -504.5134, 'y': 416.68658, 'degree': 2}, {'label': 'Perpetue', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 5.0, 'Closeness Centrality': 0.3179916317991632, 'Harmonic Closeness Centrality': 0.34956140350877174, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 3.0, 'PageRank': 0.00398765019423864, 'Component ID': 0, 'size': 10.267516, 'r': 115, 'g': 192, 'b': 0, 'x': -682.47815, 'y': 493.3663, 'degree': 2}, {'label': 'Woman1', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3958333333333333, 'Harmonic Closeness Centrality': 0.4232456140350874, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 3.0, 'PageRank': 0.003506067074877397, 'Component ID': 0, 'size': 10.267516, 'r': 115, 'g': 192, 'b': 0, 'x': -367.8953, 'y': -272.58597, 'degree': 2}, {'label': 'MotherInnocent', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39790575916230364, 'Harmonic Closeness Centrality': 0.4254385964912279, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 4.0, 'PageRank': 0.004809938914778593, 'Component ID': 0, 'size': 10.401274, 'r': 115, 'g': 192, 'b': 0, 'x': -581.59894, 'y': -291.7078, 'degree': 2}, {'label': 'MmeBurgon', 'Modularity Class': 3, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.3438914027149321, 'Harmonic Closeness Centrality': 0.37719298245614, 'Betweenness Centrality': 0.02631578947368421, 'Degree': 2, 'Weighted Degree': 3.0, 'PageRank': 0.005875948568688257, 'Component ID': 0, 'size': 10.267516, 'r': 0, 'g': 189, 'b': 148, 'x': 756.3864, 'y': -373.6602, 'degree': 2}, {'label': 'Magnon', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.33480176211453744, 'Harmonic Closeness Centrality': 0.3633771929824559, 'Betweenness Centrality': 0.0002172096908939014, 'Degree': 2, 'Weighted Degree': 2.0, 'PageRank': 0.0029861240520734633, 'Component ID': 0, 'size': 10.133758, 'r': 115, 'g': 192, 'b': 0, 'x': 21.928242, 'y': -235.35252, 'degree': 2}, {'label': 'MmePontmercy', 'Modularity Class': 2, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.3153526970954357, 'Harmonic Closeness Centrality': 0.3403508771929823, 'Betweenness Centrality': 0.0003508771929824561, 'Degree': 2, 'Weighted Degree': 2.0, 'PageRank': 0.0038396127201715076, 'Component ID': 0, 'size': 10.133758, 'r': 255, 'g': 136, 'b': 5, 'x': 517.5531, 'y': 644.42535, 'degree': 2}, {'label': 'BaronessT', 'Modularity Class': 1, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.35185185185185186, 'Harmonic Closeness Centrality': 0.3793859649122804, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 2.0, 'PageRank': 0.0029068763833626885, 'Component ID': 0, 'size': 10.133758, 'r': 115, 'g': 192, 'b': 0, 'x': 390.89252, 'y': -518.2104, 'degree': 2}, {'label': 'Child1', 'Modularity Class': 3, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.34234234234234234, 'Harmonic Closeness Centrality': 0.37499999999999967, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 5.0, 'PageRank': 0.005723750444436155, 'Component ID': 0, 'size': 10.535032, 'r': 0, 'g': 189, 'b': 148, 'x': 531.9, 'y': -650.24896, 'degree': 2}, {'label': 'Child2', 'Modularity Class': 3, 'Clustering Coefficient': 1.0, 'Number of triangles': 1, 'Eccentricity': 4.0, 'Closeness Centrality': 0.34234234234234234, 'Harmonic Closeness Centrality': 0.37499999999999967, 'Betweenness Centrality': 0.0, 'Degree': 2, 'Weighted Degree': 5.0, 'PageRank': 0.005723750444436155, 'Component ID': 0, 'size': 10.535032, 'r': 0, 'g': 189, 'b': 148, 'x': 646.4055, 'y': -517.25433, 'degree': 2}, {'label': 'Napoleon', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.003027464960131779, 'Component ID': 0, 'size': 10.0, 'r': 211, 'g': 179, 'b': 176, 'x': -613.382, 'y': -566.57275, 'degree': 1}, {'label': 'CountessDeLo', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.003027464960131779, 'Component ID': 0, 'size': 10.0, 'r': 211, 'g': 179, 'b': 176, 'x': -724.112, 'y': -423.88416, 'degree': 1}, {'label': 'Geborand', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.003027464960131779, 'Component ID': 0, 'size': 10.0, 'r': 211, 'g': 179, 'b': 176, 'x': -805.5518, 'y': -253.6047, 'degree': 1}, {'label': 'Champtercier', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.003027464960131779, 'Component ID': 0, 'size': 10.0, 'r': 211, 'g': 179, 'b': 176, 'x': 49.029377, 'y': -841.2674, 'degree': 1}, {'label': 'Cravatte', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.003027464960131779, 'Component ID': 0, 'size': 10.0, 'r': 211, 'g': 179, 'b': 176, 'x': -482.4219, 'y': -699.5888, 'degree': 1}, {'label': 'Count', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 2.0, 'PageRank': 0.00410687797221161, 'Component ID': 0, 'size': 10.133758, 'r': 211, 'g': 179, 'b': 176, 'x': -126.16586, 'y': -822.42053, 'degree': 1}, {'label': 'OldMan', 'Modularity Class': 4, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.30158730158730157, 'Harmonic Closeness Centrality': 0.3243421052631578, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.003027464960131779, 'Component ID': 0, 'size': 10.0, 'r': 211, 'g': 179, 'b': 176, 'x': -303.20972, 'y': -784.6923, 'degree': 1}, {'label': 'Labarre', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.41666666666666646, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0024843488670408254, 'Component ID': 0, 'size': 10.0, 'r': 115, 'g': 192, 'b': 0, 'x': 215.9852, 'y': -575.9705, 'degree': 1}, {'label': 'MmeDeR', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.41666666666666646, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0024843488670408254, 'Component ID': 0, 'size': 10.0, 'r': 115, 'g': 192, 'b': 0, 'x': -230.31729, 'y': -431.49188, 'degree': 1}, {'label': 'Isabeau', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.41666666666666646, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0024843488670408254, 'Component ID': 0, 'size': 10.0, 'r': 115, 'g': 192, 'b': 0, 'x': -32.993774, 'y': -447.11658, 'degree': 1}, {'label': 'Gervais', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.41666666666666646, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0024843488670408254, 'Component ID': 0, 'size': 10.0, 'r': 115, 'g': 192, 'b': 0, 'x': 212.9053, 'y': -786.5906, 'degree': 1}, {'label': 'Scaufflaire', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.39378238341968913, 'Harmonic Closeness Centrality': 0.41666666666666646, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0024843488670408254, 'Component ID': 0, 'size': 10.0, 'r': 115, 'g': 192, 'b': 0, 'x': 43.98742, 'y': -634.9646, 'degree': 1}, {'label': 'Boulatruelle', 'Modularity Class': 2, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 4.0, 'Closeness Centrality': 0.34234234234234234, 'Harmonic Closeness Centrality': 0.36293859649122784, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0024456446520771296, 'Component ID': 0, 'size': 10.0, 'r': 255, 'g': 136, 'b': 5, 'x': 181.5848, 'y': 834.5445, 'degree': 1}, {'label': 'Gribier', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.2878787878787879, 'Harmonic Closeness Centrality': 0.30460526315789466, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 2.0, 'PageRank': 0.0034984453132104595, 'Component ID': 0, 'size': 10.133758, 'r': 115, 'g': 192, 'b': 0, 'x': -852.4479, 'y': -42.990376, 'degree': 1}, {'label': 'Jondrette', 'Modularity Class': 3, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.25675675675675674, 'Harmonic Closeness Centrality': 0.27434210526315767, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.0036126324081465514, 'Component ID': 0, 'size': 10.0, 'r': 0, 'g': 189, 'b': 148, 'x': 832.5579, 'y': -186.28008, 'degree': 1}, {'label': 'MlleVaubois', 'Modularity Class': 1, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.3076923076923077, 'Harmonic Closeness Centrality': 0.32609649122807, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 1.0, 'PageRank': 0.002564659404580431, 'Component ID': 0, 'size': 10.0, 'r': 115, 'g': 192, 'b': 0, 'x': 377.09128, 'y': -743.19055, 'degree': 1}, {'label': 'MotherPlutarch', 'Modularity Class': 3, 'Clustering Coefficient': 0.0, 'Number of triangles': 0, 'Eccentricity': 5.0, 'Closeness Centrality': 0.2846441947565543, 'Harmonic Closeness Centrality': 0.3120614035087718, 'Betweenness Centrality': 0.0, 'Degree': 1, 'Weighted Degree': 3.0, 'PageRank': 0.0034930396222173947, 'Component ID': 0, 'size': 10.267516, 'r': 0, 'g': 189, 'b': 148, 'x': 672.746, 'y': 531.37177, 'degree': 1}]
    source target  weight   id
0       11      0     5.0   13
1       11      2     3.0   12
2       11      3     3.0   11
3       11     10     1.0   10
4       11     12     1.0   14
..     ...    ...     ...  ...
249     31     30     2.0   68
250      2      3     6.0    3
251     39     52     1.0  121
252     47     46     1.0  108
253     73     74     3.0  239

[254 rows x 4 columns]
             label  Modularity Class  Clustering Coefficient  \
0          Valjean                 1                0.120635   
1         Gavroche                 3                0.354978   
2           Marius                 1                0.333333   
3           Javert                 1                0.323529   
4       Thenardier                 2                0.408333   
..             ...               ...                     ...   
72    Boulatruelle                 2                0.000000   
73         Gribier                 1                0.000000   
74       Jondrette                 3                0.000000   
75     MlleVaubois                 1                0.000000   
76  MotherPlutarch                 3                0.000000   

    Number of triangles  Eccentricity  Closeness Centrality  \
0                    76           3.0              0.644068   
1                    82           3.0              0.513514   
2                    57           3.0              0.531469   
3                    44           3.0              0.517007   
4                    49           3.0              0.517007   
..                  ...           ...                   ...   
72                    0           4.0              0.342342   
73                    0           5.0              0.287879   
74                    0           5.0              0.256757   
75                    0           5.0              0.307692   
76                    0           5.0              0.284644   

    Harmonic Closeness Centrality  Betweenness Centrality  Degree  \
0                        0.732456                0.569989      36   
1                        0.605263                0.165113      22   
2                        0.603070                0.132032      19   
3                        0.585526                0.054332      17   
4                        0.581140                0.074901      16   
..                            ...                     ...     ...   
72                       0.362939                0.000000       1   
73                       0.304605                0.000000       1   
74                       0.274342                0.000000       1   
75                       0.326096                0.000000       1   
76                       0.312061                0.000000       1   

    Weighted Degree  PageRank  Component ID       size    r    g    b  \
0             158.0  0.099654             0  31.000000  115  192    0   
1              56.0  0.028256             0  17.356688    0  189  148   
2             104.0  0.051657             0  23.777071  115  192    0   
3              47.0  0.026837             0  16.152866  115  192    0   
4              61.0  0.035704             0  18.025478  255  136    5   
..              ...       ...           ...        ...  ...  ...  ...   
72              1.0  0.002446             0  10.000000  255  136    5   
73              2.0  0.003498             0  10.133758  115  192    0   
74              1.0  0.003613             0  10.000000    0  189  148   
75              1.0  0.002565             0  10.000000  115  192    0   
76              3.0  0.003493             0  10.267516    0  189  148   

            x           y  degree  
0  -125.47393  -77.948814      36  
1   468.20163   19.530542      22  
2   354.36575  180.876740      19  
3  -234.89421  102.362270      17  
4   131.99199  460.775880      16  
..        ...         ...     ...  
72  181.58480  834.544500       1  
73 -852.44790  -42.990376       1  
74  832.55790 -186.280080       1  
75  377.09128 -743.190550       1  
76  672.74600  531.371770       1  

[77 rows x 19 columns]
(77, 19)
(77, 19)

Yes, you are more likely to be interested in exporting the nexworkx graph to use in Gephi. You can do that as well. Here is the code.

Code 
import networkx as nx
# Export the graph as graphML file
nx.write_graphml(gephi_graph, "lesmis2.graphml")
# Export the graph as Gephi file
nx.write_gexf(gephi_graph, "lesmis2.gexf")

Lastly, you might be interested in importing node and edge tables into Gephi.

Alt Text
Figure 5: Importing node and edge tables.

references

1: Stamile, Claudio, et al. Graph Machine Learning : Take Graph Data to the Next Level by Applying Machine Learning Techniques and Algorithms, Packt Publishing, Limited, 2021

2: Static and dynamic network visualization with R